Answer:
A
Explanation:
Solution:-
- First we will go through the guidelines that are followed when a given function [ f ( x ) ] is translated in a cartesian coordinate system domain.
Horizontal shifts:
- Left shift: f ( x ) - > f ( x + a ).
- Right Shift: f ( x ) - > f ( x - a )
Where, the constant ( a ) denotes the magnitude of shift
Vertical shifts:
- Up shift: f ( x ) - > f ( x ) + b
- Down Shift: f ( x ) - > f ( x ) - b
Where, the constant ( b ) denotes the magnitude of shift
- The generalized form of a translated function is defined by the combination of both horizontal and vertical shifts as follows:
General: f ( x ) -> f ( x ± a ) ± b
Where, (a) and (b) are constants of respective translation shifts.
- We are given a function H ( x ) is to be translated 3 units to right and 3 units down. Use the above guidelines to determine the translated function H* ( x ) as follows:
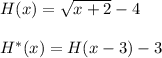
- Substitute ( x - 3 ) in place of all ( x ) in the given function H ( x ) and subtract ( 3 ) from H ( x ) as follows:
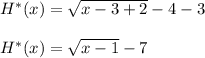
- Now we will look for any transcendental functions in the translated function H*(x). These are " Radicals, fractions, Logs, trigonometric ratios "
- We have a radical - > " square root " in H* ( x ). To find the domain of H*(x) we need to determine for what real values of x is the function H*(x) is defined.
- The square root exist for all only positive numbers. So the terms under the square root must be positive; hence,
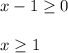
- Since the square root is the only transcendental in the given function H*(x) we have a one sided closed interval for the domain of the translated function.
Domain: [ 1 , ∞ ) ... Answer
- The range of the function is the corresponding output of function H*(x) for the domain established above. We can determine this by plugging in the end-points of the defined domain in the translated function H*(x) as follows:
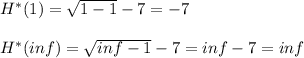
Therefore the range of the function is also a one sided closed interval bounded by x = 1.
Range: [-7 , ∞ ) ... Answer