Question

Did this several times but still didn't get the answer .pls do try this :)​

Answer 1

x=-15/2 and x=1

x=6 and x=3/4

Explanation:

You have the following equations:

`(4x-3)/(x+2)=(2x)/(x+5)`

`(2)/(x-2)+(3)/(x)-(9)/(x+3)`

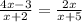
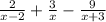
To solve both equations you can first multiply by the m.c.m of the denominators, and then solve for x, just as follow:

first equation:

`[(4x-3)/(x+2)=(2x)/(x+5)](x+2)(x+5)\\\\(4x-3)(x+5)=2x(x+2)\\\\4x(x)+4x(5)-3(x)-3(5)=2x(x)+2x(2)\\\\4x^2+20x-3x-15=2x^2+4x\\\\4x^2-2x^2+20x-3x-4x-15=0\\\\2x^2+13x-15=0`

In this case you use the quadratic formula:

`x_(1,2)=(-13\pm √((13)^2-4(2)(-15)))/(2(2))\\\\x_(1,2)=(-13 \pm 17)/(4)\\\\x_1=-(15)/(2)\\\\x_2=1`

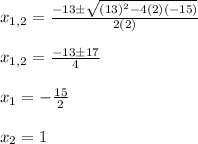
Then, for the first equation the solutions are x=-15/2 and x=1

second equation:

`[(2)/(x-2)+(3)/(x)=(9)/(x+3)]x(x-2)(x+3)\\\\2x(x+3)+3(x-2)(x+3)=9x(x-2)\\\\2x^2+6x+3(x^2+3x-2x-6)=9x^2-18x\\\\2x^2+6x+3(x^2+x-6)=9x^2-18x\\\\2x^2+6x+3x^2+3x-18-9x^2+18x=0\\\\-4x^2+27x-18=0`

Again, you use the quadratic formula:

`x_(1,2)=(-27\pm √((27)^2-4(-4)(-18)))/(2(-4))\\\\x_(1,2)=(-27\pm 21)/(-8)\\\\x_1=6\\\\x_2=(3)/(4)`

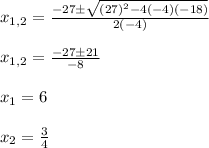
Then, the solutions for the second equation are x=6 and x=3/4