Question

Please Help!!!

Family Size. You selected a random sample of n = 31 families in your neighborhood and found the mean family size for the sample equal to 3.1, the standard deviation for the sample is 1.42? What is the 90% confidence interval for the estimate?

Answer 1

Answer : (2.67, 3.53)

Step to step explanation:

Confidence interval for mean, when population standard deviation is unknown:

`\overline{x}\pm t_(\alpha/2)(s)/(√(n))`

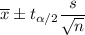
, where
`\overline{x}` = sample mean

n= sample size

s= sample standard deviation

`t_(\alpha/2)` = Critical t-value for n-1 degrees of freedom

We assume the family size is normal distributed.

Given, n= 31 ,
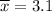`\overline{x}=3.1`, s= 1.42 ,

`\alpha=1-0.9=0.10`

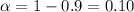
Critical t value for
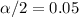`\alpha/2=0.05` and degree of 30 freedom

`t_(\alpha/2)` = 1.697 [By t-table]

The required confidence interval:

`3.1\pm ( 1.697)(1.42)/(√(31))\\\\=3.1\pm0.4328\\\\=(3.1-0.4328,\ 3.1+0.4328)=(2.6672,\ 3.5328)\approx(2.67,\ 3.53)`

Hence, the 90% confidence interval for the estimate = (2.67, 3.53)