Answer : (2.67, 3.53)
Step to step explanation:
Confidence interval for mean, when population standard deviation is unknown:
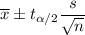
, where
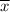 = sample mean
= sample mean
n= sample size
s= sample standard deviation
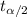 = Critical t-value for n-1 degrees of freedom
= Critical t-value for n-1 degrees of freedom
We assume the family size is normal distributed.
Given, n= 31 ,
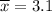 , s= 1.42 ,
, s= 1.42 ,
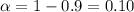
Critical t value for
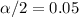 and degree of 30 freedom
and degree of 30 freedom
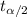 = 1.697 [By t-table]
= 1.697 [By t-table]
The required confidence interval:
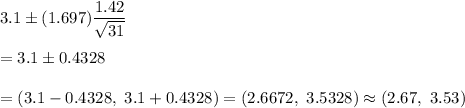
Hence, the 90% confidence interval for the estimate = (2.67, 3.53)