Answer:
the required stress level at which fracture will occur for a critical internal crack length of 3.0 mm is 189.66 MPa
Step-by-step explanation:
From the given information; the objective is to compute the stress level at which fracture will occur for a critical internal crack length of 3.0 mm.
The Critical Stress for a maximum internal crack can be expressed by the formula:
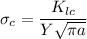
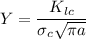
where;
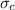 = critical stress required for initiating crack propagation
= critical stress required for initiating crack propagation
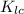 = plain stress fracture toughness = 26 Mpa
= plain stress fracture toughness = 26 Mpa
Y = dimensionless parameter
a = length of the internal crack
given that ;
the maximum internal crack length is 8.6 mm
half length of the internal crack will be 8.6 mm/2 = 4.3mm
half length of the internal crack a = 4.3 × 10⁻³ m
From :
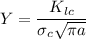
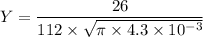
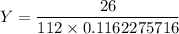
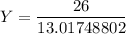
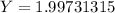
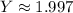
For this same component and alloy, we are to also compute the stress level at which fracture will occur for a critical internal crack length of 3.0 mm.
when the length of the internal crack a = 3mm
half length of the internal crack will be 3.0 mm / 2 = 1.5 mm
half length of the internal crack a =1.5 × 10⁻³ m
From;
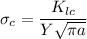
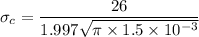
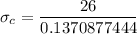

 189.66 MPa
189.66 MPa
Thus; the required stress level at which fracture will occur for a critical internal crack length of 3.0 mm is 189.66 MPa