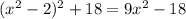Answer:
(D)
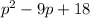
Explanation:
Assuming that the equation
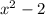 = p, we can convert the equation into this.
= p, we can convert the equation into this.
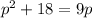
We can convert
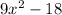 into 9p because
into 9p because
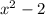 × 9 =
× 9 =
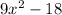
Now we simplify this equation.
We can subtract 9p from both sides of the equation.
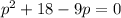
Re-ordering the equation gets us:
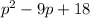
So, (D)
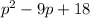 is equivalent to the original expression of
is equivalent to the original expression of