Question

Which point on the graph of g(x)=(1/5)^x? HELPP

Answer 1

(-1,5) and
`(3, (1)/(125))` are points on the graph

Explanation:

Given

`g(x) = (1)/(5)^x`

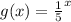
Required

Determine which point in on the graph

To get which of point A to D is on the graph, we have to plug in their values in the given expression using the format; (x,g(x))

A. (-1,5)

x = -1

Substitute -1 for x in
`g(x) = (1)/(5)^x`

`g(x) = (1)/(5)^(-1)`

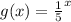
Convert to index form

`g(x) = 1/((1)/(5))`

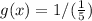
Change / to *

`g(x) = 1*((5)/(1))`

`g(x) = 5`

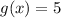
This satisfies (-1,5)

Hence, (-1,5) is on the graph

B. (1,0)

x = 1

Substitute 1 for x

`g(x) = (1)/(5)^x`

`g(x) = (1)/(5)^1`

`g(x) = (1)/(5)`

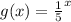
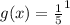
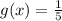
(1,0) is not on the graph because g(x) is not equal to 0

C.
`(3, (1)/(125))`

x = 3

Substitute 3 for x

`g(x) = (1)/(5)^x`

`g(x) = (1)/(5)^3`

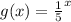
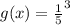
Apply law of indices

`g(x) = (1)/(5) * (1)/(5) * (1)/(5)`

`g(x) = (1)/(125)`

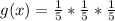
This satisfies
`(3, (1)/(125))`

Hence,
`(3, (1)/(125))` is on the graph

D.
`(-2, (1)/(25))`

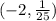
x = -2

Substitute -2 for x

`g(x) = (1)/(5)^x`

`g(x) = (1)/(5)^(-2)`

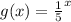
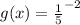
Convert to index form

`g(x) = 1/((1)/(5)^2)`

`g(x) = 1/((1)/(5)*(1)/(5))`

`g(x) = 1/((1)/(25))`

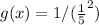
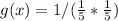
Change / to *

`g(x) = 1*((25)/(1))`

`g(x) = 25`

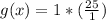
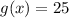
This does not satisfy
`(-2, (1)/(25))`

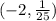
Hence,
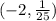`(-2, (1)/(25))` is not on the graph