Answer:

Step-by-step explanation:
There are two heat transfers involved: the heat lost by the aluminium and the heat gained by the water.
According to the Law of Conservation of Energy, energy can neither be destroyed nor created, so the sum of these terms must be zero.
Let the Al be Component 1 and the H₂O be Component 2.
Data:
For the Al:
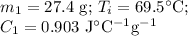
For the water:
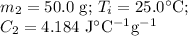
Calculations
(a) The relative temperature changes
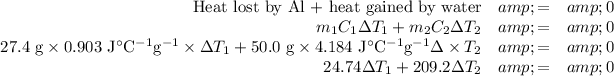
(b) Final temperature
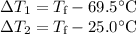

Check:
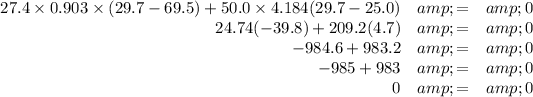
The second term has only two significant figures because ΔT₂ has only two.
It agrees to two significant figures