Question

A box with a hinged lid is to be made out of a rectangular piece of cardboard that measures 3 centimeters by 5 centimeters. Six squares will be cut from the cardboard: one square will be cut from each of the corners, and one square will be cut from the middle of each of the -5 centimeter sides . The remaining cardboard will be folded to form the box and its lid . Letting x represent the side-lengths (in centimeters) of the squares, to find the value of that maximizes the volume enclosed by this box. Then give the maximum volume. Round your responses to two decimal places.

Answer 1

x = 0.53 cm

Maximum volume = 1.75 cm³

Step-by-step explanation:

Refer to the attached diagram:

The volume of the box is given by

`V = Length * Width * Height \\\\`

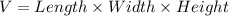
Let x denote the length of the sides of the square as shown in the diagram.

The width of the shaded region is given by

`Width = 3 - 2x \\\\`

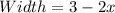
The length of the shaded region is given by

`Length = (1)/(2) (5 - 3x) \\\\`

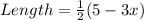
So, the volume of the box becomes,

`V = (1)/(2) (5 - 3x) * (3 - 2x) * x \\\\V = (1)/(2) (5 - 3x) * (3x - 2x^2) \\\\V = (1)/(2) (15x -10x^2 -9 x^2 + 6 x^3) \\\\V = (1)/(2) (6x^3 -19x^2 + 15x) \\\\`

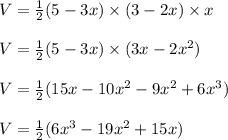
In order to maximize the volume enclosed by the box, take the derivative of volume and set it to zero.

`(dV)/(dx) = 0 \\\\(dV)/(dx) = (d)/(dx) ( (1)/(2) (6x^3 -19x^2 + 15x)) \\\\(dV)/(dx) = (1)/(2) (18x^2 -38x + 15) \\\\(dV)/(dx) = (1)/(2) (18x^2 -38x + 15) \\\\0 = (1)/(2) (18x^2 -38x + 15) \\\\18x^2 -38x + 15 = 0 \\\\`

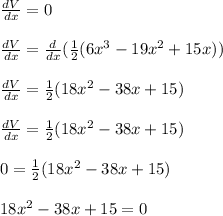
We are left with a quadratic equation.

We may solve the quadratic equation using quadratic formula.

The quadratic formula is given by

`$x=(-b\pm√(b^2-4ac))/(2a)$`

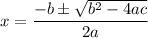
Where

`a = 18 \\\\b = -38 \\\\c = 15 \\\\`

`x=(-(-38)\pm√((-38)^2-4(18)(15)))/(2(18)) \\\\x=(38\pm√((1444- 1080))/(36) \\\\x=(38\pm√((364))/(36) \\\\x=(38\pm 19.078)/(36) \\\\x=(38 + 19.078)/(36) \: or \: x=(38 - 19.078)/(36)\\\\x= 1.59 \: or \: x = 0.53 \\\\`

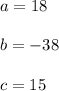
Volume of the box at x= 1.59:

`V = (1)/(2) (5 – 3(1.59)) * (3 - 2(1.59)) * (1.59) \\\\V = -0.03 \: cm^3 \\\\`

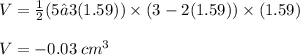
Volume of the box at x= 0.53:

`V = (1)/(2) (5 – 3(0.53)) * (3 - 2(0.53)) * (0.53) \\\\V = 1.75 \: cm^3`

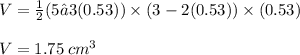
The volume of the box is maximized when x = 0.53 cm

Therefore,

x = 0.53 cm

Maximum volume = 1.75 cm³