Answer:
x = 0.53 cm
Maximum volume = 1.75 cm³
Step-by-step explanation:
Refer to the attached diagram:
The volume of the box is given by
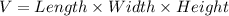
Let x denote the length of the sides of the square as shown in the diagram.
The width of the shaded region is given by
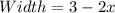
The length of the shaded region is given by
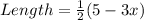
So, the volume of the box becomes,
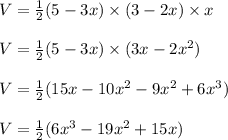
In order to maximize the volume enclosed by the box, take the derivative of volume and set it to zero.
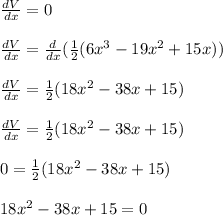
We are left with a quadratic equation.
We may solve the quadratic equation using quadratic formula.
The quadratic formula is given by
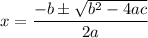
Where
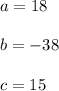

Volume of the box at x= 1.59:
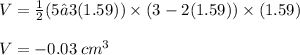
Volume of the box at x= 0.53:

The volume of the box is maximized when x = 0.53 cm
Therefore,
x = 0.53 cm
Maximum volume = 1.75 cm³