Question

Complete the table of values below: x -3 -2 -1 0 1 2 3 How the graph relates to y=2x y=2x Answer Answer Answer Answer Answer Answer Answer Not applicable y=-2x Answer Answer Answer Answer Answer Answer Answer multiplied by Answer y=(3)(2x)

Answer 1

a y = 2^x

> x = -3

=> y = 2^(-3) = 1/8

> x = -2

=> y = 2^(-2) = 1/4

> x = -1

=> y = 2^(-1) = 1/2

> x = 0

=> y = 2^0 = 1

> x = 1

=> y = 2^1 = 2

> x = 2

=> y = 2^2 = 4

> x = 3

=> y = 2^3 = 8

b. y = -2^x

> x = -3

=> y = -2^(-3) = -1/8

> x = -2

=> y = -2^(-2) = -1/4

> x = -1

=> y = -2^(-1) = -1/2

> x = 0

=> y = -2^0 = -1

> x = 1

=> y = -2^1 = -2

> x = 2

=> y = -2^2 = -4

> x = 3

=> y = -2^3 = -8

c. y = (3)(2^x)

> x = -3

=> y = 3 * 2^(-3) = 3 * 1/8 = 3/8

> x = -2

=> y = 3 * 2^(-2) = 3 * 1/4 = 3/4

> x = -1

=> y = 3 * 2^(-1) = 3 * 1/2 = 3/2

> x = 0

=> y = 3 * 2^0 = 3 * 1 = 3

> x = 1

=> y = 3 * 2^1 = 3 * 2 = 6

> x = 2

=> y = 3 * 2^2 = 3 * 4 = 12

> x = 3

=> y = 3 * 2^3 = 3 * 8 = 24

Explanation:

Answer 2

The values of x are:

x : -3, -2, -1, 0, 1, 2, 3

Let's solve each by putting each value of x into each equation:

a
`y = 2^x`

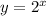
> x = -3

=> y = 2^(-3) = 1/8

> x = -2

=> y = 2^(-2) = 1/4

> x = -1

=> y = 2^(-1) = 1/2

> x = 0

=> y = 2^0 = 1

> x = 1

=> y = 2^1 = 2

> x = 2

=> y = 2^2 = 4

> x = 3

=> y = 2^3 = 8

b.
`y = -2^x`

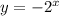
> x = -3

=> y = -2^(-3) = -1/8

> x = -2

=> y = -2^(-2) = -1/4

> x = -1

=> y = -2^(-1) = -1/2

> x = 0

=> y = -2^0 = -1

> x = 1

=> y = -2^1 = -2

> x = 2

=> y = -2^2 = -4

> x = 3

=> y = -2^3 = -8

c.
`y = (3)(2^x)`

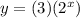
> x = -3

=> y = 3 * 2^(-3) = 3 * 1/8 = 3/8

> x = -2

=> y = 3 * 2^(-2) = 3 * 1/4 = 3/4

> x = -1

=> y = 3 * 2^(-1) = 3 * 1/2 = 3/2

> x = 0

=> y = 3 * 2^0 = 3 * 1 = 3

> x = 1

=> y = 3 * 2^1 = 3 * 2 = 6

> x = 2

=> y = 3 * 2^2 = 3 * 4 = 12

> x = 3

=> y = 3 * 2^3 = 3 * 8 = 24

Input these values into the table.