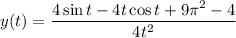1 Answer

Motorcb · Answer 1 · 2021-10-25T10:05:00+0000

For the ODE

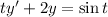
$ty'+2y=\sin t$

multiply both sides by t so that the left side can be condensed into the derivative of a product:

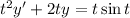
$t^2y'+2ty=t\sin t$

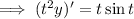
$\implies(t^2y)'=t\sin t$

Integrate both sides with respect to t :

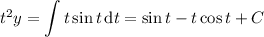
$t^2y=\displaystyle\int t\sin t\,\mathrm dt=\sin t-t\cos t+C$

Divide both sides by
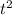t^2 to solve for y :

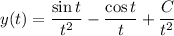
$y(t)=(\sin t)/(t^2)-\frac{\cos t}t+\frac C{t^2}$

Now use the initial condition to solve for C :

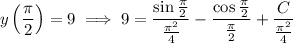
$y\left(\frac\pi2\right)=9\implies9=\frac{\sin\frac\pi2}{\frac{\pi^2}4}-(\cos\frac\pi2)/(\frac\pi2)+\frac C{\frac{\pi^2}4}$

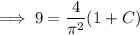
$\implies9=\frac4{\pi^2}(1+C)$

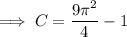
$\implies C=\frac{9\pi^2}4-1$

So the particular solution to the IVP is

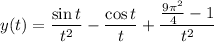
$y(t)=(\sin t)/(t^2)-\frac{\cos t}t+\frac{\frac{9\pi^2}4-1}{t^2}$

or

$y(t)=(4\sin t-4t\cos t+9\pi^2-4)/(4t^2)$

Please log in or register to add a comment.