Answer:
The y-value is z = 0.759 m
Step-by-step explanation:
From the question we are told that
The position of the first y-axis is
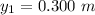
The current on the first wire is
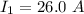
The force per unit length on each wire is

Generally the force per unit length on first wire is mathematically represented as
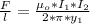
Where
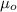 is the permeability of free space with value
is the permeability of free space with value
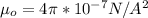
substituting values
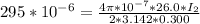
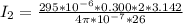
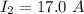
Now the at the point where the magnetic field is zero the magnetic field of each wire are equal , let that point by z meters from the second wire on the y-axis so
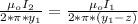
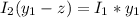
substituting values
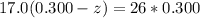
z = 0.759 m