Two cars leave an intersection at the same time. One drives east while the other travels south at 15 miles per hour faster than the other. After 3 hours, the cars are 225 miles …

Question

asked Dec 23, 2021 230k views

1 Answer

Tinylee · Answer 1 · 2021-12-27T22:02:40+0000

Answer:

60 mph

Explanation:

Let 'S' be the velocity of the southbound car and 'E' be the velocity of the eastbound car. The distances traveled by each car are:

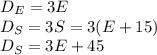
$D_E=3E\\D_S=3S=3(E+15)\\D_S=3E+45$

The distance between both cars is given by:

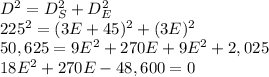
$D^2=D_S^2+D_E^2\\225^2=(3E+45)^2+(3E)^2\\50,625=9E^2+270E+9E^2+2,025\\18E^2+270E-48,600=0\\$

Solving the quadratic equation for the velocity of the eastbound car:

$18E^2+270E-48,600=0\\E^2+15E-2,700\\E=(-15\pm√(15^2-4*1*(-2,700)))/(2)\\E=45.0\ mph$

The velocity of the southbound car is:

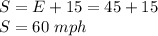
$S=E+15=45+15\\S=60\ mph$

The southbound car is driving at 60 mph.