Question

Benzene boils at 80.10 °C and has a molal boiling constant, k b, of 2.53 C/m. When 2.15 g of a compound is dissolved in 20.0 g of benzene, the resulting solution has a boiling point of 81.10 °C. What is the molality of the solute?

Answer 1

`m=0.395mol/kg`

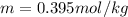
Step-by-step explanation:

Hello,

This is a problem about boiling point elevation which is modeled via:

`\Delta T=i*m*Kb`

Whereas for this solvent (nonpolar, nonionizing), the van't Hoff factor is one. In such a way, the molality of the solute is simply computed as shown below:

`m=(\Delta T)/(Kb)=((81.10-80.10)\°C)/(2.53\°C/m) \\\\m=0.395mol/kg`

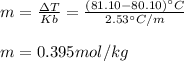
In this manner, we can also compute the molar mass of the solute by noticing 20.0 g (0.020 kg) of benzene were used:

`n=0.395mol/kg*0.020kg=7.9x10^(-3) mol`

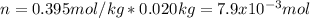
And considering the 2.15 g of the solute:

`Molar\ mass=(2.15g)/(7.9x10^(-3)mol)\\ \\Molar\ mass=271.975g/mol`

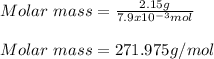
Best regards.