Answer:
25 -
![\sqrt[4]{26.66*10^(-8) }](https://img.qammunity.org/2021/formulas/engineering/college/q4kig8zuyz2xuxjm43k32m8wa6tu1wmgg4.png) mm
mm
Step-by-step explanation:
Given data
steel tube : outer diameter = 50-mm
power transmitted = 100 KW
frequency(f) = 34 Hz
shearing stress ≤ 60 MPa
Determine tube thickness
firstly we calculate the ; power, angular velocity and torque of the tube
power = T(torque) * w (angular velocity)
angular velocity ( w ) = 2
 f = 2 *
f = 2 *
 * 34 = 213.71
* 34 = 213.71
Torque (T) = power / angular velocity = 100000 / 213.71 = 467.92 N.m/s
next we calculate the inner diameter using the relation
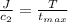 = 467.92 / (60 * 10^6) = 7.8 * 10^-6 m^3
= 467.92 / (60 * 10^6) = 7.8 * 10^-6 m^3
also
c2 = (50/2) = 25 mm
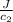 =
=
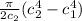 =
=
![(\pi )/(0.050) [ ( 0.025^(4) - c^(4) _(1) ) ]](https://img.qammunity.org/2021/formulas/engineering/college/74x94j6gf3t2usrc6olkvgh3zqucvfqn8u.png)
therefore; 0.025^4 -
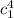 = 0.050 /
= 0.050 /
 (7.8 *10^-6)
(7.8 *10^-6)
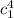 = 39.06 * 10 ^-8 - ( 1.59*10^-2 * 7.8*10^-6)
= 39.06 * 10 ^-8 - ( 1.59*10^-2 * 7.8*10^-6)
39.06 * 10^-8 - 12.402 * 10^-8 =26.66 *10^-8
![c_(1) = \sqrt[4]{26.66 * 10^(-8) }](https://img.qammunity.org/2021/formulas/engineering/college/ugew19sajj2be2zhtlr0sdnsqvmkolbryy.png) =
=
THE TUBE THICKNESS
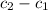 = 25 -
= 25 -
![\sqrt[4]{26.66*10^(-8) }](https://img.qammunity.org/2021/formulas/engineering/college/q4kig8zuyz2xuxjm43k32m8wa6tu1wmgg4.png) mm
mm