Answer:
The two inequalities are;
P ≤ 90e^(0.047t)
P ≤ 270 + 100·t
Explanation:
The parameters given for the testing of the new growth inhibitor are;
The growth rate of the bacteria = 4.7% exponentially
The growth inhibitor lowers the growth rate
The population of bacteria after time, t = P
The increase in the number of bacteria per unit time in the 100
The maximum number of bacteria in the standard tube = 270
Therefore, the number of bacteria after the first filling of the tube is P ≤ 270 + 100·t
The equation for exponential growth is
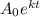
Where:
A₀ = Initial population = 90
k = Percentage growth rate as percentage
t = Time
The equation for the population of bacteria under the influence of the inhibitor is therefore;
P ≤
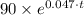 which is P ≤ 90e^(0.047t).
which is P ≤ 90e^(0.047t).