Question

Identify the distance between points (3,8, 0) and (-2,9,-4), and identify the midpoint of the

segment for which these are the endpoints. Round to the nearest tenth if necessary
A) d-3.5 units; M(-0.5, 8.5.2)
B) d-3.5 units; M(0.5, 8.5.-2)
C) d-6.5 units: M(0.5, 8.5.-2)
D) d-6.5 units: M(-0.5, 8.5.2)

Answer 1

Answer: C) d-6.5 units: M(0.5, 8.5.-2)

Explanation:

Distance between points
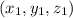`(x_1,y_1,z_1)` and
`(x_2,y_2,z_2)` :

`D=√((x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2)`

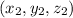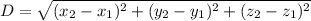
The midpoint of the line joining
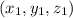`(x_1,y_1,z_1)` and
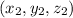`(x_2,y_2,z_2)` is given by :-

`((x_1+x_2)/(2),(y_1+y_2)/(2),(z_1+z_2)/(2))`

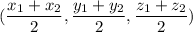
The given points : (3,8, 0) and (-2,9,-4)

Distance between points (3,8, 0) and (-2,9,-4):

`D=√((-2-3)^2+(9-8)^2+(-4-0)^2)\\\\=√(25+1+16)\\\\=√(42)=6.48074069841\approx6.5\text{units}`

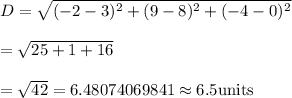
The midpoint of the line joining (3,8, 0) and (-2,9,-4) :

`((3+(-2))/(2),(8+9)/(2),(0+(-4))/(2))=((1)/(2),(17)/(2),-2)\\\\=(0.5, 8.5.-2)`

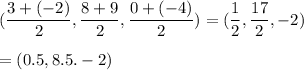
Hence, the correct answer is C) d-6.5 units: M(0.5, 8.5.-2).