Question

Waves with an amplitude of 2 feet pass a dock every 30 seconds. Write an equation for a cosine function to model the height of a water particle above and below the mean water line. Explain your steps.

Answer 1

The cosine function to model the height of a water particle above and below the mean water line is h = 2·cos((π/30)·t)

Explanation:

The cosine function equation is given as follows h = d + a·cos(b(x - c))

Where:

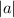`\left | a \right |` = Amplitude

2·π/b = The period

c = The phase shift

d = The vertical shift

h = Height of the function

x = The time duration of motion of the wave, t

The given data are;

The amplitude
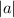`\left | a \right |` = 2 feet

Time for the wave to pass the dock

The number of times the wave passes a point in each cycle = 2 times

Therefore;

The time for each complete cycle = 2 × 30 seconds = 60 seconds

The time for each complete cycle = Period = 2·π/b = 60

b = π/30 =

Taking the phase shift as zero, (moving wave) and the vertical shift as zero (movement about the mean water line), we have

h = 0 + 2·cos(π/30(t - 0)) = 2·cos((π/30)·t)

The cosine function is h = 2·cos((π/30)·t).