Answer:
- 0.26
- 0.91
- 1.43
Explanation:
given data
mean = 1.9 hours
standard deviation = 0.3 hours
solution
we get here first random movie between 1.8 and 2.0 hours
so here
P(1.8 < z < 2 )
z = (1.8 - 1.9) ÷ 0.3
z = -0.33
and
z = (2.0 - 1.9) ÷ 0.3
z = 0.33
z = 0.6293
so
P(-0.333 < z < 0.333 )
= 0.26
so random movie is between 1.8 and 2.0 hours long is 0.26
and
A movie is longer than 2.3 hours.
P(x > 2.3)
P(
 >
>
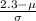 )
)
P (z >
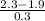 )
)
P (z > 1.333 )
= 0.091
so chance a movie is longer than 2.3 hours is 0.091
and
length of movie that is shorter than 94% of the movies is
P(x > a ) = 0.94
P(x < a ) = 0.06
so
P(
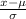 <
<
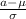 )
)

a = 1.43
so length of the movie that is shorter than 94% of the movies about 1.4 hours.