Question

The volume of a right circular cone with both

2507
diameter and height equal to his What is the
3
value of h?
A) 5
B) 10
C) 20
D) 40

Answer 1

Question:

The volume of a right circular cone with both diameter and height equal to h is 250/7 cm³.

What is the value of h?

Answer:

A. 5

Explanation:

Given

Solid Shape: Cone

Volume = 250/7

Diameter = Height

Required

Find the height of the cone

Provided that the diameter (D) and the height (h) are equal; This implies that

D = h ------ (1)

Also, Diameter (D) = 2 * Radius (r)

D = 2r

Substitute 2r for D in (1)

2r = h

Multiply both sides by ½

½ * 2r = ½ * h

r = ½h

Volume of a cone is calculated by;

Volume = ⅓πr²h

⅓πr²h = 250/7

Substitute ½h for r

`(1)/(3) * \pi * ((1)/(2)h)^2 * h = (250)/(7)`

Take π as 22/7, the expression becomes

`(1)/(3) * (22)/(7) * ((1)/(2)h)^2 * h = (250)/(7)`

Open the bracket

`(1)/(3) * (22)/(7) * (1)/(4)h^2 * h = (250)/(7)`

Multiply both sides by 7

`7 * (1)/(3) * (22)/(7) * (1)/(4)h^2 * h = (250)/(7) * 7`

`(1)/(3) * 22 * (1)/(4)h^2 * h = 250`

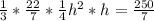
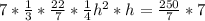
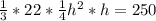
Multiply both sides by 3

`3 * (1)/(3) * 22 * (1)/(4)h^2 * h = 250 * 3`

`22 * (1)/(4)h^2 * h = 750`

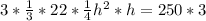
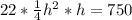
Multiply both sides by 4

`4 * 22 * (1)/(4)h^2 * h = 750 * 4`

`22 * h^2 * h = 3000`

`22 * h^3 = 3000`

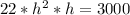
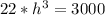
Divide both sides by 22

`h^3 = (3000)/(22)`

`h^3 = 136.36`

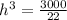
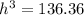
Take cube root of both sides

`h = \sqrt[3]{136.36}`

`h = 5.15`

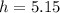
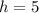`h = 5` (Approximated)