Question

let x = the amoun of raw sugar in tons a procesing plant is a sugar refinery process in one day . suppose x can be model as exponetial distribution with mean of 4 ton per day . The amount of raw sugar (x) has

Answer 1

The answer is below

Explanation:

A sugar refinery has three processing plants, all receiving raw sugar in bulk. The amount of raw sugar (in tons) that one plant can process in one day can be modelled using an exponential distribution with mean of 4 tons for each of three plants. If each plant operates independently,a.Find the probability that any given plant processes more than 5 tons of raw sugar on a given day.b.Find the probability that exactly two of the three plants process more than 5 tons of raw sugar on a given day.c.How much raw sugar should be stocked for the plant each day so that the chance of running out of the raw sugar is only 0.05?

Answer: The mean (μ) of the plants is 4 tons. The probability density function of an exponential distribution is given by:

`f(x)=\lambda e^(-\lambda x)\\But\ \lambda= 1/\mu=1/4 = 0.25\\Therefore:\\f(x)=0.25e^(-0.25x)\\`

a) P(x > 5) =
`\int\limits^\infty_5 {f(x)} \, dx =\int\limits^\infty_5 {0.25e^(-0.25x)} \, dx =-e^(-0.25x)|^\infty_5=e^(-1.25)=0.2865`

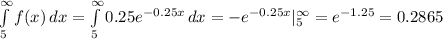
b) Probability that exactly two of the three plants process more than 5 tons of raw sugar on a given day can be solved when considered as a binomial.

That is P(2 of the three plant use more than five tons) = C(3,2) × [P(x > 5)]² × (1-P(x > 5)) = 3(0.2865²)(1-0.2865) = 0.1757

c) Let b be the amount of raw sugar should be stocked for the plant each day.

P(x > a) =
`\int\limits^\infty_a {f(x)} \, dx =\int\limits^\infty_a {0.25e^(-0.25x)} \, dx =-e^(-0.25x)|^\infty_a=e^(-0.25a)`

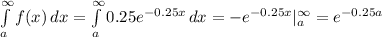
But P(x > a) = 0.05

Therefore:

`e^(-0.25a)=0.05\\ln[e^(-0.25a)]=ln(0.05)\\-0.25a=-2.9957\\a=11.98`

a ≅ 12