Answer:
The equation representing the new path is;
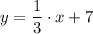
Explanation:
The equation of the first walking park across the park is y = -3·x - 3
By comparison to the equation of a straight line, y = m·x + c, where m = the slope of the line, the slope of the line y = -3·x - 3 is -3
The park's new walking path direction = Perpendicular to first walking path
A line perpendicular to a line of (as example) y = m₁·x + c has a slope of -1/m
∴ The park's new walking path slope = -1/(Slope of first path) = -1/(-3) = 1/3
The point the paths will intersect = (-3, 6)
The equation of the line is found by recalling that
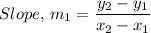
Where:
y₂ and x₂ are coordinates of a point on the new walking path
y₁ and x₁ are coordinates of a point on the new walking path intersecting the first walking path
Given that (-3, 6) is the intersection of the two walking paths, therefore, it is a point on the new walking path and we can say x₁ = -3, y₁ = 6
Therefore, we have;

Which gives;
(y₂ - 6) × 3 = x₂ + 3
y₂ - 6 = (x₂ + 3)/3
y₂ = (x₂ + 3)/3 + 6 = 1/3·x₂ + 1 + 6 = 1/3·x₂ + 7
Which gives the equation representing the new path as
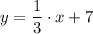 .
.