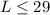Question

The perimeter of an equilateral triangle must be at most 57 feet. Create an inequality to find

what the length of the sides should be. Solve the inequality by showing all of your work and
explaining each step. Explain your answer.

Answer 1

`L \leq 29`

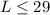
Explanation:

Given

Perimeter = 57 (at most)

Required

Determine the length of each side

The term at most in the values of the perimeter shows that the expression is an inequality and it means that perimeter can't exceed that value;

Let L represents the length of each sides;

Perimeter = L + L + L

So,

`L + L + L \leq 57`

`3 L \leq 57`

Divide both sides by 3

`3 L/3 \leq 57/3`

`L \leq 29`