Answer:
 283.181 hp
283.181 hp
Step-by-step explanation:
Given that:
Air enters a compressor operating at steady state at a pressure
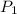 = 176.4 lbf/in.^2 and Temperature
= 176.4 lbf/in.^2 and Temperature
 at 260°F
at 260°F
Volumetric flow rate V = 424 ft^3/min
Air exits at a pressure
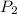 = 15.4 lbf/in.^2 and Temperature
= 15.4 lbf/in.^2 and Temperature
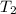 at 80°F.
at 80°F.
Heat transfer occurs at a rate of 6800 Btu/h from the compressor to its surroundings; since heat is released to the surrounding; then:
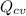 = -6800 Btu/h = - 1.9924 kW
= -6800 Btu/h = - 1.9924 kW
Using the steady state energy in the process;
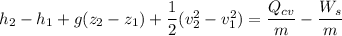
where;
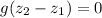 and
and
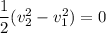
Then; we have :
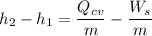
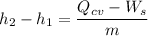

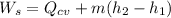 ----- (1)
----- (1)
Using the relation of Ideal gas equation;
P₁V₁ = mRT₁
Pressure
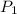 = 176.4 lbf/in.^2 = ( 176.4 × 6894.76 ) N/m² = 1216235.664 N/m²
= 176.4 lbf/in.^2 = ( 176.4 × 6894.76 ) N/m² = 1216235.664 N/m²
Volumetric flow rate V = 424 ft^3/min = (424 × 0.0004719) m³ /sec
= 0.2000856 m³ /sec
Temperature = 260°F = (260°F − 32) × 5/9 + 273.15 = 399.817 K
Gas constant R=287 J/kg K
Then;
1216235.664 N/m² × 0.2000856 m³ /sec = m × 287 J/kg K × 399.817 K
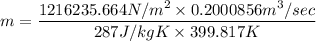
m = 2.121 kg/sec
The change in enthalpy:
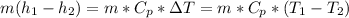
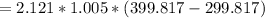
= 213.1605 kW
From (1)
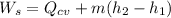
 - 1.9924 kW + 213.1605 kW
- 1.9924 kW + 213.1605 kW
 211.1681 kW
211.1681 kW
 283.181 hp
283.181 hp
The power input is
 283.181 hp
283.181 hp