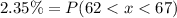Question

The time it takes to drive from Orangeville to the Vaughan Mills Mall is normally distributed with a mean of 52 minutes and standard deviation of 5 minutes. What intervals could you estimate, using the knowledge from this activity that do not include the mean as a max or min? For example, is an interval we could estimate? However, it includes the mean as the maximum of the interval. Another example is as an example of a probability interval that we know from this activity, but it includes the mean as the minimum.

Answer 1

Given:

Mean of 52 minutes and a standard deviation of 5 minutes.

Solution:

According to the empirical rule: For the normal distribution, all of the data will fall within three standard deviations of the mean.

1: 68% of the data will fall within the first standard deviation from the mean.

2: 95% of the data fall within two standard deviations.

3: 99.7% of the data fall within three standard deviations.

`3SD =99.7\%=\mu\pm3\sigma\\`

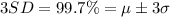
Therefore, the 7 intervals and their probabilities are:

1.
`1SD=0.68=P(47<x<57)`

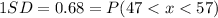
2.
`0.95=P(42<x<62)`

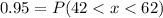
3.
`0.997=P(37<x<67)`

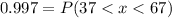
4.
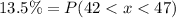
`13.5\%=P(42<x<47)`

5.
`13.5\%=P(57<x<62)`

6.
`2.35\%=P(37<x<42)`

7.
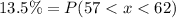
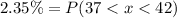
`2.35\%=P(62<x<67)`