Complete question:
Two cars start moving from the same point. One travels south at 28 mi/h and the other travels west at 21 mi/h. At what rate is the distance between the cars increasing four hours later.
Answer:
The rate at which the distance between the cars is increasing four hours later is 35 mi/h.
Step-by-step explanation:
Given;
speed of one car, dx/dt = 28 mi/h South
speed of the second car, dy/dt = 21 mi/h West
The distance between the cars is the line joining west to south, which forms a right angled triangle with the two positions.
Apply Pythagoras theorem to evaluate this distance;
let the distance between the cars = z
x² + y² = z² -------- equation (1)
Differentiate with respect to time (t)
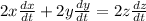 ----- equation (2)
----- equation (2)
Since the speed of the cars is constant, after 4 hours their different distance will be;
x: 28(4) = 112 mi
y: 21(4) = 84 mi
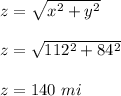
Substitute in the value of x, y, z, dx/dt, dy /dt into equation (2) and solve for dz/dt
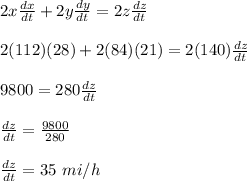
Therefore, the rate at which the distance between the cars is increasing four hours later is 35 mi/h