Question

Two cars start moving from the same point. One travels south at 28 mi/h and the other travels west at 21 mi/h. At what rate is the distance between the cars increasin

Answer 1

Complete question:

Two cars start moving from the same point. One travels south at 28 mi/h and the other travels west at 21 mi/h. At what rate is the distance between the cars increasing four hours later.

Answer:

The rate at which the distance between the cars is increasing four hours later is 35 mi/h.

Step-by-step explanation:

Given;

speed of one car, dx/dt = 28 mi/h South

speed of the second car, dy/dt = 21 mi/h West

The distance between the cars is the line joining west to south, which forms a right angled triangle with the two positions.

Apply Pythagoras theorem to evaluate this distance;

let the distance between the cars = z

x² + y² = z² -------- equation (1)

Differentiate with respect to time (t)

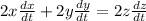`2x(dx)/(dt) + 2y(dy)/(dt) = 2z(dz)/(dt)` ----- equation (2)

Since the speed of the cars is constant, after 4 hours their different distance will be;

x: 28(4) = 112 mi

y: 21(4) = 84 mi

`z = √(x^2 + y^2) \\\\z = √(112^2 + 84^2) \\\\z = 140 \ mi`

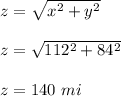
Substitute in the value of x, y, z, dx/dt, dy /dt into equation (2) and solve for dz/dt

`2x(dx)/(dt) + 2y(dy)/(dt) = 2z(dz)/(dt) \\\\2(112)(28) + 2(84)(21) = 2(140)(dz)/(dt) \\\\9800 = 280(dz)/(dt) \\\\(dz)/(dt) = (9800)/(280) \\\\(dz)/(dt) = 35 \ mi/h`

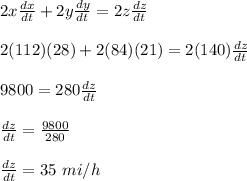
Therefore, the rate at which the distance between the cars is increasing four hours later is 35 mi/h