Answer:
3.47 and 3.21
Explanation:
Let us assume the nails length be X
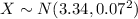
Value let separated the top 3% is T and for bottom it would be B
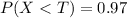
Now converting, we get
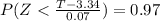
Based on the normal standard tables, we get

Now compare these two above equations
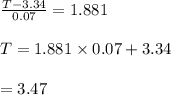
So for top 3% it is 3.47
Now for bottom we applied the same method as shown above

Based on the normal standard tables, we get
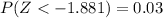
Now compare these two above equations
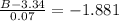
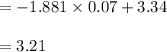
hence, for bottom it would be 3.21