Answer:
24.25
Explanation:
The minimum admission score is at the 70th percentile of the normal distribution which, according to a z-score table, corresponds to a z-score of 0.524.
The z-score, for any given value X, is determined by:
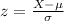
If the mean score is 21 and the standard distribution is 6.2, the minimum required score for admission is:
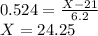
The minimum score required for admission is 24.25.