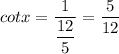Question

If 12 5 )tan( = x and π

Answer 1

`sinx=-(12)/(13)`

`cosx=-(5)/(13)`

`cotx=(5)/(12)`

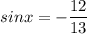
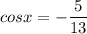
Explanation:

Given that:

`(12)/(5) = tan(x)`

`\pi <x < 3\pi/2`

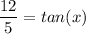
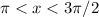
i.e. x is in 3rd quadrant. So tan is positive.

To find:

sin(x), cos(x), and cot(x).

Solution:

Given that:

`(12)/(5) = tan(x)`

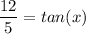
We know by trigonometric identities that:

`tan\theta =(Perpendicular)/(Base)`

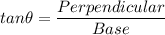
Comparing with the given values:

`\theta=x`

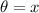
Perpendicular = 12 units

Base = 5 units

Using pythagorean theorem, we can find out hypotenuse:

According to pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)`

`\Rightarrow Hypotenuse=√(12^2+5^2)\\\Rightarrow Hypotenuse=√(169) = 13 units`

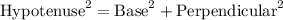
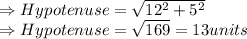
We can easily find out the values of:

`sinx, cos x\ and\ cot x`

`sin\theta =(Perpendicular)/(Hypotenuse)`

`sinx =(12)/(13)`

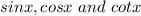
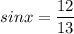
Given that x is in 3rd quadrant, sinx will be negative.

`\therefore sinx =-(12)/(13)`

`sin\theta =(Base)/(Hypotenuse)`

`cosx =(5)/(13)`

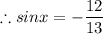
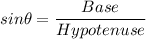
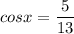
Given that x is in 3rd quadrant, cosx will be negative.

`\therefore cosx =-(5)/(13)`

`cot\theta = (1)/(tan\theta)`

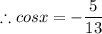
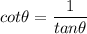
Given that x is in 3rd quadrant, cotx will be positive.

`cotx = (1)/((12)/(5)) = (5)/(12)`