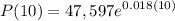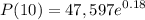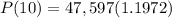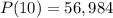Given Information:
Starting population = P₀ = 47,597
rate of growth = 1.8%
Required Information:
Equation that defines the population t years = ?
Answer:
The following equation defines the population t years after 2010.
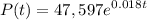
Step-by-step explanation:
The population growth can be modeled as an exponential function,
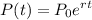
Where P₀ is the starting population in 2010, r is the rate of growth of the population and t is the time in years after 2010.
We are given that the starting population is 47,597 and rate of growth is 1.8%
So the population function becomes
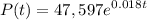
Therefore, the above function may be used to estimate the population for t years after 2010.
For example:
What is the population after 10 years?
For the given case,
t = 10