Question

A window washer is standing on a scaffold supported by a vertical rope at each end. The scaffold weighs 210 N and is 2.8 m long. What is the tension in each rope when the 698-N worker stands 1.80 m from one end?

Answer 1

The value of tension in the two ropes are 354.2 N and 553.8 N

Step-by-step explanation:

Find the free body diagram attached below.

For the system to be in mechanical equilibrium, the following conditions have to be satisfied.

1. Upward forces must be equals to the downward forces,

T1 + T2 =210N + 698N

`T1 + T2 =908 ------------------ equation 1`

2. Clock-wise turning moments = anti-clockwise turning moments

`T1 * 2.8 = 210N * 1.4m + 698N* (2.8 - 1.8)\\2.8T1 =294Nm + 698Nm\\2.8T1 =992Nm\\T1 = (992)/(2.8)=354.2 N`

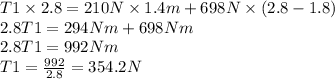
From this, we were able to evaluate the value of T1 by taking our moments about T2 as the turning point

We can input the value of T1 into equation 1 to give us the value of T2 as

T2 = 908 - T1

T2 = 908 - 354.2N= 553.8 N

There fore, the value of tension in the two ropes are 354.2 N and 553.8 N