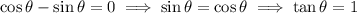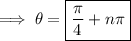Q.04: (11 points) Given the polar curve r = e θ , where 0 ≤ θ ≤ 2π. Find points on the curve in the form (r, θ) where there is a horizontal or vertical tangent line. g

Question

asked Jan 23, 2021 56.2k views

1 Answer

Sean Redmond · Answer 1 · 2021-01-27T14:07:32+0000

I suppose the curve is
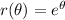$r(\theta)=e^\theta$ .

Tangent lines to the curve have slope
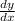(dy)/(dx) ; use the chain rule to get this in polar coordinates.

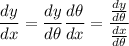
$(dy)/(dx)=(dy)/(d\theta)(d\theta)/(dx)=((dy)/(d\theta))/((dx)/(d\theta))$

We have

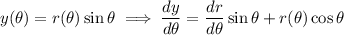
$y(\theta)=r(\theta)\sin\theta\implies(dy)/(d\theta)=(dr)/(d\theta)\sin\theta+r(\theta)\cos\theta$

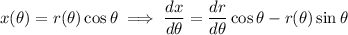
$x(\theta)=r(\theta)\cos\theta\implies(dx)/(d\theta)=(dr)/(d\theta)\cos\theta-r(\theta)\sin\theta$

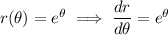
$r(\theta)=e^\theta\implies(dr)/(d\theta)=e^\theta$

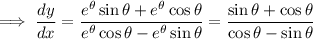
$\implies(dy)/(dx)=(e^\theta\sin\theta+e^\theta\cos\theta)/(e^\theta\cos\theta-e^\theta\sin\theta)=(\sin\theta+\cos\theta)/(\cos\theta-\sin\theta)$

The tangent line is horizontal when the slope is 0, which happens wherever the numerator vanishes:

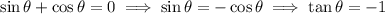
$\sin\theta+\cos\theta=0\implies\sin\theta=-\cos\theta\implies\tan\theta=-1$

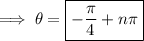
$\implies\theta=\boxed{-\frac\pi4+n\pi}$

(where
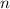is any integer)

The tangent line is vertical when the slope is infinite or undefined, which happens when the denominator is 0:

$\cos\theta-\sin\theta=0\implies\sin\theta=\cos\theta\implies\tan\theta=1$

$\implies\theta=\boxed{\frac\pi4+n\pi}$