Question

prove the following identity: sec x csc x(tan x + cot x) = 2+tan^2 x + cot^2 x please provide a proof in some shape form or fashion :/

Answer 1

Explanation:

Hello,

Is this equality true ?

sec x csc x(tan x + cot x) = 2+tan^2 x + cot^2 x

1. let 's estimate the left part of the equation

`sec(x)csc(x)(tan(x) + cot(x)) =(1)/(cos(x)sin(x))*((sin(x))/(cos(x))+(cos(x))/(sin(x)))\\\\=(1)/(cos(x)sin(x))*((sin^2(x)+cos^2(x))/(sin(x)cos(x)))\\\\=(1)/(cos(x)sin(x))*((1)/(sin(x)cos(x)))\\\\\\=(1)/(cos^2(x)sin^2(x))`

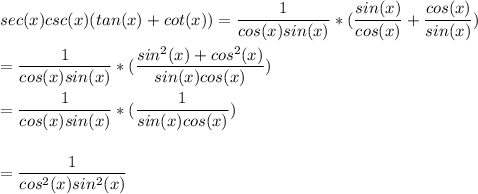
1. let 's estimate the right part of the equation

`2+tan^2(x) + cot^2(x)=2+(sin^2(x))/(cos^2(x))+(cos^2(x))/(sin^2(x))\\\\=(2cos^2(x)sin^2(x)+cos^4(x)+sin^4(x))/(cos^2(x)sin^2(x))\\\\=((cos^2(x)+sin^2(x))^2)/(cos^2(x)sin^2(x))\\\\=(1^2)/(cos^2(x)sin^2(x))\\\\=(1)/(cos^2(x)sin^2(x))`

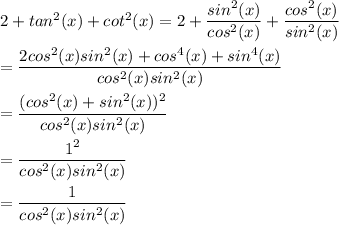
This is the same expression

So

sec x csc x(tan x + cot x) = 2+tan^2 x + cot^2 x

hope this helps