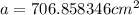Question

Need help again thanks guys!!

Answer 1

225π cm^2, 706.5 cm^2, 706.858... cm^2

Explanation:

The area of a circle can be found using the following equation:

`a=\pi r^2`

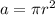
We know the radius is 15 cm, so we can substitute 15 cm in for r.

`a=\pi (15cm)^2`

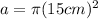
1. In terms of pi

To find the area in terms of pi, evaluate everything possible without multiplying by pi.

Evaluate the exponent.

`a=\pi (15cm)^2`

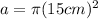
15cm^2= 15 cm * 15 cm = 225 cm^2

`a=\pi * 225 cm^2`

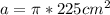
This can be rewritten as:

`a=225\pi cm^2`

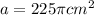
2. Using 3.14 for pi

Substitute 3.14 in for pi.

`a=\pi (15cm)^2`

`a=3.14*(15cm)^2`

`a=3.14*225 cm^2`

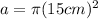
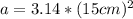
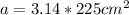
Multiply

`a=706.5 cm^2`

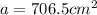
3. Using 3.14159265.... as pi

`a=\pi (15cm)^2`

`a=\pi *225 cm^2`

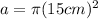
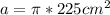
Multiply, using the pi button on a calculator

`a=706.858346 cm^2`

Answer 2

A = 225 pi cm^2

Using 3.14 for pi

A =706.5 cm^2

Using the pi button for pi

A =706.8583471 cm^2

Explanation:

The area of a circle is

A = pi r^2

A = pi (15)^2

A = 225 pi cm^2

Using 3.14 for pi

A =706.5 cm^2

Using the pi button for pi

A =706.8583471 cm^2