Question

You are at the carnival with you your little brother and you decide to ride the bumper cars for fun. You each get in a different car and before you even get to drive your car, the little brat crashes into you at a speed of 3 m/s.

A. Knowing that the bumper cars each weigh 80 kg, while you and your brother weigh 60 and 30 kg,respectively, write down the equations you need to use to figure out how fast you and your brother are moving after the collision.
B. After the collision, your little brother reverses direction and moves at 0.36 m/s. How fast are you moving after the collision?
C. Assuming the collision lasted 0.05 seconds, what is the average force exerted on you during the collision?
D. Who undergoes the larger acceleration, you or your brother? Explain.

Answer 1

a) The equation is
`(m_(b)+m_(c) )u_(b) = (m_(y)+m_(c) )v_(y) + (m_(b)+m_(c) )v_(b)`

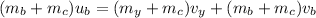
b) Your velocity after collision is 2.64 m/s

c) The force you felt is 7392 N

d) you and your brother undergo an equal amount of acceleration

Step-by-step explanation:

Your mass
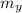`m_(y)` = 60 kg

your brother's mass
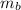`m_(b)` = 30 kg

mass of the car
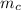`m_(c)` = 80 kg

your initial speed
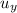`u_(y)` = 0 m/s (since you've not started moving yet)

your brother's initial velocity
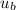`u_(b)` = 3 m/s

your final speed
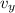`v_(y)` after collision = ?

your brother's final speed
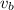`v_(b)` after collision = ?

a) equations you need to use to figure out how fast you and your brother are moving after the collision is

`(m_(y)+m_(c) )u_(y) + (m_(b)+m_(c) )u_(b) = (m_(y)+m_(c) )v_(y) + (m_(b)+m_(c) )v_(b)`

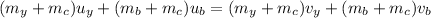
but
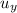`u_(y)` = 0 m/s

the equation reduces to

`(m_(b)+m_(c) )u_(b) = (m_(y)+m_(c) )v_(y) + (m_(b)+m_(c) )v_(b)`

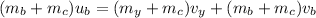
b) if your little brother reverses with velocity of 0.36 m/s it means

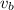`v_(b)` = -0.36 m/s (the reverse means it travels in the opposite direction)

then, imputing values into the equation, we'll have

`(m_(b)+m_(c) )u_(b) = (m_(y)+m_(c) )v_(y) + (m_(b)+m_(c) )v_(b)`

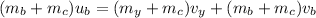
(30 + 80)3 = (60 + 80)
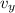`v_(y)` + (30 + 80)(-0.36)

330 = 140
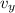`v_(y)` - 39.6

369.6 = 140
`v_(y)`

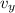
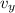`v_(y)` = 369.6/140 = 2.64 m/s

This means you will also reverse with a velocity of 2.64 m/s

c) your initial momentum = 0 since you started from rest

your final momentum = (total mass) x (final velocity)

==> (60 + 80) x 2.64 = 369.6 kg-m/s

If the collision lasted for 0.05 s,

then force exerted on you = (change in momentum) ÷ (time collision lasted)

force on you = ( 369.6 - 0) ÷ 0.05 = 7392 N

d) you changed velocity from 0 m/s to 2.64 m/s in 0.05 s

your acceleration is (2.64 - 0)/0.05 = 52.8 m/s^2

your brother changed velocity from 3 m/s to 0.36 m/s in 0.05 s

his deceleration is (3 - 0.36)/0.05 = 52.8 m/s

you and your brother undergo an equal amount of acceleration. This is because you gained the momentum your brother lost