Answer:
a) The equation is
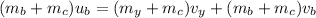
b) Your velocity after collision is 2.64 m/s
c) The force you felt is 7392 N
d) you and your brother undergo an equal amount of acceleration
Step-by-step explanation:
Your mass
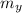 = 60 kg
= 60 kg
your brother's mass
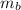 = 30 kg
= 30 kg
mass of the car
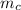 = 80 kg
= 80 kg
your initial speed
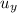 = 0 m/s (since you've not started moving yet)
= 0 m/s (since you've not started moving yet)
your brother's initial velocity
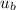 = 3 m/s
= 3 m/s
your final speed
 after collision = ?
after collision = ?
your brother's final speed
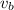 after collision = ?
after collision = ?
a) equations you need to use to figure out how fast you and your brother are moving after the collision is
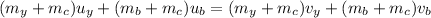
but
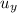 = 0 m/s
= 0 m/s
the equation reduces to
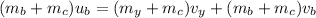
b) if your little brother reverses with velocity of 0.36 m/s it means
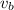 = -0.36 m/s (the reverse means it travels in the opposite direction)
= -0.36 m/s (the reverse means it travels in the opposite direction)
then, imputing values into the equation, we'll have
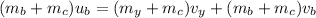
(30 + 80)3 = (60 + 80)
 + (30 + 80)(-0.36)
+ (30 + 80)(-0.36)
330 = 140
 - 39.6
- 39.6
369.6 = 140

 = 369.6/140 = 2.64 m/s
= 369.6/140 = 2.64 m/s
This means you will also reverse with a velocity of 2.64 m/s
c) your initial momentum = 0 since you started from rest
your final momentum = (total mass) x (final velocity)
==> (60 + 80) x 2.64 = 369.6 kg-m/s
If the collision lasted for 0.05 s,
then force exerted on you = (change in momentum) ÷ (time collision lasted)
force on you = ( 369.6 - 0) ÷ 0.05 = 7392 N
d) you changed velocity from 0 m/s to 2.64 m/s in 0.05 s
your acceleration is (2.64 - 0)/0.05 = 52.8 m/s^2
your brother changed velocity from 3 m/s to 0.36 m/s in 0.05 s
his deceleration is (3 - 0.36)/0.05 = 52.8 m/s
you and your brother undergo an equal amount of acceleration. This is because you gained the momentum your brother lost