Answer:
i) A = (3, 3), B = (12, 6), C = (6, 52) : Not orthogonal, ii) A = (-10, 5), B = (12, 16), C = (6, 52) : Not orthogonal, iii) A = (-8, 3), B = (12, 8), C = (18, 4) : Not orthogonal, iv) A = (12, -14), B = (-16, 21), C = (-11, 25) : Orthogonal, v) A = (-12, -19), B = (20, 45) : Impossible orthogonality, vi) A = (30, 20), B = (-20, -15) : Impossible orthogonality.
Explanation:
The statement indicates that segments AB and BC must be orthogonal. Vectorially speaking, this can be expressed by using the following expression from Linear Algebra:
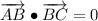
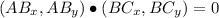
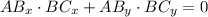
Now, let is evaluate each choice:
i) A = (3, 3), B = (12, 6), C = (6, 52)
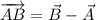
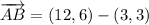

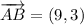
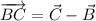
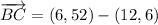
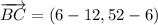
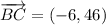
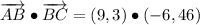


AB and BC are not orthogonal.
ii) A = (-10, 5), B = (12, 16), C = (6, 52)
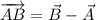
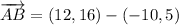
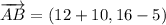
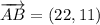
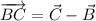
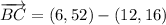
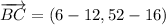
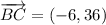
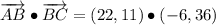

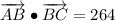
AB and BC are not orthogonal.
iii) A = (-8, 3), B = (12, 8), C = (18, 4)
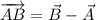
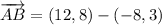


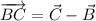
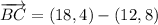
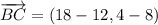
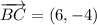
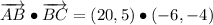
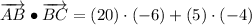
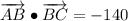
AB and BC are not orthogonal.
iv) A = (12, -14), B = (-16, 21), C = (-11, 25)
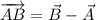
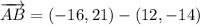
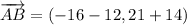
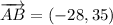
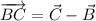

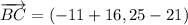

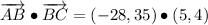
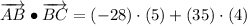
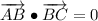
AB and BC are orthogonal.
v) A = (-12, -19), B = (20, 45)
It is not possible to determine the orthogonality of this solution, since point C is unknown.
vi) A = (30, 20), B = (-20, -15)
It is not possible to determine the orthogonality of this solution, since point C is unknown.