Question

Match each pair of points A and B to point C such that ∠ABC = 90°. A(3, 3) and B(12, 6) C(6, 52) A(-10, 5) and B(12, 16) C(16, -6) A(-8, 3) and B(12, 8) C(18, 4) A(12, -14) and B(-16, 21) C(-11, 25) A(-12, -19) and B(20, 45) A(30, 20) and B(-20, -15) arrowBoth arrowBoth arrowBoth arrowBoth

Answer 1

i) A = (3, 3), B = (12, 6), C = (6, 52) : Not orthogonal, ii) A = (-10, 5), B = (12, 16), C = (6, 52) : Not orthogonal, iii) A = (-8, 3), B = (12, 8), C = (18, 4) : Not orthogonal, iv) A = (12, -14), B = (-16, 21), C = (-11, 25) : Orthogonal, v) A = (-12, -19), B = (20, 45) : Impossible orthogonality, vi) A = (30, 20), B = (-20, -15) : Impossible orthogonality.

Explanation:

The statement indicates that segments AB and BC must be orthogonal. Vectorially speaking, this can be expressed by using the following expression from Linear Algebra:

`\overrightarrow {AB} \bullet \overrightarrow {BC} = 0`

`(AB_(x), AB_(y))\bullet (BC_(x),BC_(y)) = 0`

`AB_(x)\cdot BC_(x) + AB_(y)\cdot BC_(y) = 0`

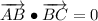
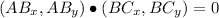
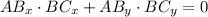
Now, let is evaluate each choice:

i) A = (3, 3), B = (12, 6), C = (6, 52)

`\overrightarrow {AB} = \vec B - \vec A`

`\overrightarrow {AB} = (12, 6) - (3, 3)`

`\overrightarrow {AB} = (12-3, 6-3)`

`\overrightarrow {AB} = (9, 3)`

`\overrightarrow {BC} = \vec C - \vec B`

`\overrightarrow {BC} = (6, 52) - (12, 6)`

`\overrightarrow {BC} = (6 - 12, 52 - 6)`

`\overrightarrow {BC} = (-6, 46)`

`\overrightarrow {AB} \bullet \overrightarrow {BC} = (9, 3)\bullet (-6, 46)`

`\overrightarrow{AB} \bullet \overrightarrow {BC} = (9)\cdot (-6) + (3) \cdot (46)`

`\overrightarrow{AB}\bullet \overrightarrow {BC} = 84`

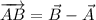
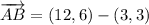
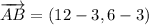
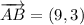
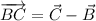
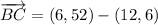
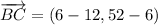
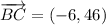
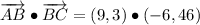
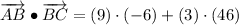
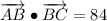
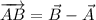
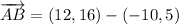
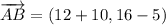
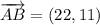
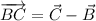
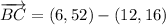
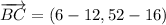
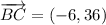
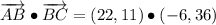
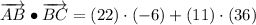
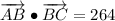
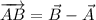
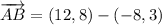
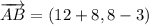
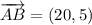
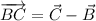
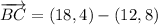
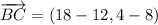
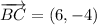
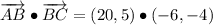
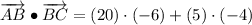
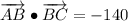
AB and BC are not orthogonal.

ii) A = (-10, 5), B = (12, 16), C = (6, 52)

`\overrightarrow {AB} = \vec B - \vec A`

`\overrightarrow {AB} = (12, 16) - (-10, 5)`

`\overrightarrow {AB} = (12+10, 16-5)`

`\overrightarrow {AB} = (22, 11)`

`\overrightarrow {BC} = \vec C - \vec B`

`\overrightarrow {BC} = (6, 52) - (12, 16)`

`\overrightarrow {BC} = (6 - 12, 52 - 16)`

`\overrightarrow {BC} = (-6, 36)`

`\overrightarrow {AB} \bullet \overrightarrow {BC} = (22, 11)\bullet (-6, 36)`

`\overrightarrow{AB} \bullet \overrightarrow {BC} = (22)\cdot (-6) + (11) \cdot (36)`

`\overrightarrow{AB}\bullet \overrightarrow {BC} = 264`

AB and BC are not orthogonal.

iii) A = (-8, 3), B = (12, 8), C = (18, 4)

`\overrightarrow {AB} = \vec B - \vec A`

`\overrightarrow {AB} = (12, 8) - (-8, 3)`

`\overrightarrow {AB} = (12+8, 8-3)`

`\overrightarrow {AB} = (20, 5)`

`\overrightarrow {BC} = \vec C - \vec B`

`\overrightarrow {BC} = (18, 4) - (12, 8)`

`\overrightarrow {BC} = (18 - 12, 4 - 8)`

`\overrightarrow {BC} = (6, -4)`

`\overrightarrow {AB} \bullet \overrightarrow {BC} = (20, 5)\bullet (-6, -4)`

`\overrightarrow{AB} \bullet \overrightarrow {BC} = (20)\cdot (-6) + (5) \cdot (-4)`

`\overrightarrow{AB}\bullet \overrightarrow {BC} = -140`

AB and BC are not orthogonal.

iv) A = (12, -14), B = (-16, 21), C = (-11, 25)

`\overrightarrow {AB} = \vec B - \vec A`

`\overrightarrow {AB} = (-16,21) - (12, -14)`

`\overrightarrow {AB} = (-16-12, 21+14)`

`\overrightarrow {AB} = (-28, 35)`

`\overrightarrow {BC} = \vec C - \vec B`

`\overrightarrow {BC} = (-11,25) - (-16, 21)`

`\overrightarrow {BC} = (-11+16, 25-21)`

`\overrightarrow {BC} = (5, 4)`

`\overrightarrow {AB} \bullet \overrightarrow {BC} = (-28,35)\bullet (5, 4)`

`\overrightarrow{AB} \bullet \overrightarrow {BC} = (-28)\cdot (5) + (35) \cdot (4)`

`\overrightarrow{AB}\bullet \overrightarrow {BC} = 0`

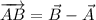
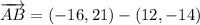
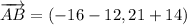
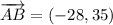
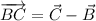
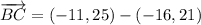
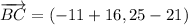
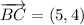
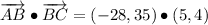
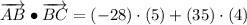
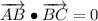
AB and BC are orthogonal.

v) A = (-12, -19), B = (20, 45)

It is not possible to determine the orthogonality of this solution, since point C is unknown.

vi) A = (30, 20), B = (-20, -15)

It is not possible to determine the orthogonality of this solution, since point C is unknown.