Answer:
The 95% confidence interval for true average degree of polymerization is (431, 446).
Explanation:
The data provided for the degree of polymerization for paper specimens for which viscosity times concentration fell in a certain middle range is:
S = {418, 421, 422, 422, 425, 429, 431, 434, 437, 439, 446, 447, 449, 452, 457, 461, 465}
Compute the sample mean and sample standard deviation:
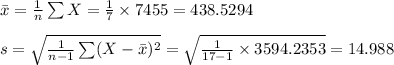
As the population standard deviation is not provided use the t-statistic to compute the two-sided 95% confidence interval for true average degree of polymerization.

The critical value of the t is:
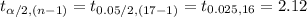
*Use a t-table.
Compute the 95% confidence interval for true average as follows:
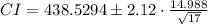

Thus, the 95% confidence interval for true average degree of polymerization is (431, 446).