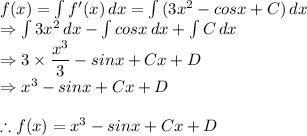Question

Find f. (Use C for the constant of the first antiderivative and D for the constant of the second antiderivative.)

f ''(x)= 6x +sinx

Answer 1

`f(x) = x^3 -sinx +Cx+D`

Explanation:

Given that:

`f ''(x)= 6x +sinx`

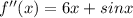
We are given the 2nd derivative of a function f(x) and we need to find f(x) from that.

We will have to integrate it twice to find the value of f(x).

Let us have a look at the basic formula of integration that we will use in the solution:

`1.\ \int {(a\pm b)} \, dx =\int {a} \, dx + \int {b} \, dx \\2.\ \int {x^n} \, dx = (x^(n+1))/(n+1)+C\\3.\ \int {sinx} \, dx = -cosx+C\\4.\ \int {cosx} \, dx = sinx+C`

`\int\ {f''(x)} \, dx =\int\ {(6x +sinx)} \, dx \\\Rightarrow \int\ {6x} \, dx + \int\ {sinx} \, dx \\\\\Rightarrow 6(x^2)/(2) -cosx +C\\\Rightarrow 3{x^2} -cosx +C\\\Rightarrow f'(x)=3{x^2} -cosx +C\\`

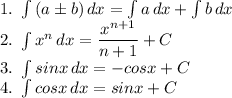
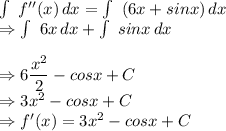
Now, integrating it again to find f(x):

`f(x) =\int {f'(x)} \, dx =\int{(3{x^2} -cosx +C)} \, dx \\\Rightarrow \int{3{x^2}} \, dx -\int{cosx} \, dx +\int{C} \, dx\\\Rightarrow 3* (x^3)/(3) -sinx +Cx+D\\\Rightarrow x^3 -sinx +Cx+D\\\\\therefore f(x) = x^3 -sinx +Cx+D`