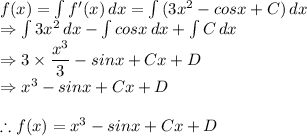Answer:
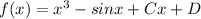
Explanation:
Given that:
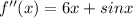
We are given the 2nd derivative of a function f(x) and we need to find f(x) from that.
We will have to integrate it twice to find the value of f(x).
Let us have a look at the basic formula of integration that we will use in the solution:
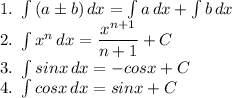
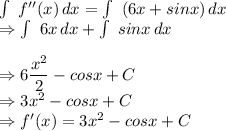
Now, integrating it again to find f(x):