Question

Suppose a shipment of stereos contained 6% defectives. If a sample of size 285 is selected, what is the probability that the sample proportion will differ from the population proportion by less than 4%? Round your answer to four decimal places. 20 points.

Answer 1

0.9954

Step-by-step explanation:

For normal distribution z score is

=
`(\hat p-p)/(\sigma p)`

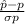
Population proportion (p) = 0.060

Sample size (n) = 285

the standard error of proportion is

=
`\sigma p = \sqrt{(p* (1 - p))/(n)}`

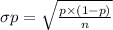
After putting the values into the above formula we will get

= 0.0141

Probability as the sample proportion will different from the population proportion by lower than the 4% that is

Probability = P(0.02<X<0.1) = P(-2.84<Z<2.84) = 0.9977 - 0.0023

= 0.9954