Question

What is the difference?

StartFraction x Over x squared minus 2 x minus 15 EndFraction minus StartFraction 4 Over x squared + 2 x minus 35 EndFraction

StartFraction x squared + 3 x + 12 Over (x minus 3) (x minus 5) (x + 7) EndFraction

StartFraction x (x + 3 minus 12) Over (x + 3) (x minus 5) (x + 7) EndFraction

StartFraction x squared + 3 x + 12 Over (x + 3) (x minus 5) (x + 7) EndFraction

StartFraction x squared + 3 x minus 12 Over (x + 3) (x minus 5) (x + 7) EndFraction

Answer 1

D

Explanation:

Answer 2

D.
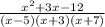`(x^(2)+3x-12 )/((x-5)(x+3)(x+7)) \\` or StartFraction x squared + 3 x minus 12 Over (x + 3) (x minus 5) (x + 7) EndFraction

Explanation:

Given the expression
`(x)/(x^(2)-2x-15 ) - (4)/(x^(2) + 2x - 35 )`, the dfference is expressed as follows;

Step1: First we need to factorize the denominator of each function.

`(x)/(x^(2)-2x-15 ) - (4)/(x^(2) + 2x - 35 )\\= (x)/(x^(2)-5x+3x-15 ) - (4)/(x^(2) + 7x-5x - 35 )\\= (x)/(x(x-5)+3(x-5) ) - (4)/(x( x+ 7)x-5(x +7) )\\= (x)/((x-5)(x+3) ) - (4)/((x-5)(x +7) )\\\\`

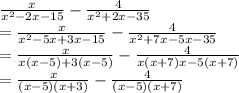
Step 2: We will find the LCM of the resulting expression

`= (x)/((x-5)(x+3) ) - (4)/((x-5)(x +7) )\\= (x(x+7)-4(x+3))/((x-5)(x+3)(x+7)) \\= (x^(2)+7x-4x-12 )/((x-5)(x+3)(x+7)) \\= (x^(2)+3x-12 )/((x-5)(x+3)(x+7)) \\`

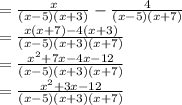
The final expression gives the difference