Answer:
D.
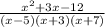 or StartFraction x squared + 3 x minus 12 Over (x + 3) (x minus 5) (x + 7) EndFraction
or StartFraction x squared + 3 x minus 12 Over (x + 3) (x minus 5) (x + 7) EndFraction
Explanation:
Given the expression
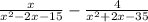 , the dfference is expressed as follows;
, the dfference is expressed as follows;
Step1: First we need to factorize the denominator of each function.
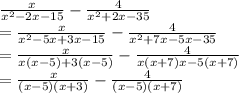
Step 2: We will find the LCM of the resulting expression
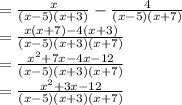
The final expression gives the difference