Answer:
a)
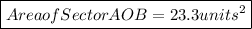
b)
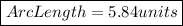
Explanation:
a) Area of Sector AOB =
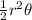
Where r = 8, θ = 41.8 degrees
Firstly, Angle in Radians
=> 41.8 degrees = 0.73 radians
So,
Area of Sector AOB =
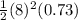
Area of Sector AOB =
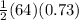
Area of Sector AOB = 23.3 units²
b) Finding the length of minor arc AB
So,
Arc Length = Radius ×
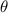
Where Radius = 8,
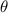 = 0.73 radians
= 0.73 radians
Arc Length AB = 8 * 0.73
Arc Length = 5.84 units