Question

Find the thickness of the material that will allow heat transfer of 6706.8 *10^6 kcal during the 5 months through the rectangle heater made from copper whose dimensions are 450 cm by 384 cm. Outside and inside temperature are 30° C and 50° C respectively

Answer 1

The thickness of the material is 6.23 cm

Step-by-step explanation:

Given;

quantity of heat, Q = 6706.8 *10⁶ kcal

duration of the heat transfer, t = 5 months

thermal conductivity of copper, k = 385 W/mk

outside temperature of the heater, T₁ = 30° C

inside temperature of the heater, T₂ = 50° C

dimension of the rectangular heater = 450 cm by 384 cm

1 kcal = 1.163000 Watt-hour

6706.8 *10⁶ kcal = 7800008400 watt-hour

I month = 730 hours

5 months = 3650 hours

Rate of heat transfer, P =
`(7800008400 \ Watt-Hour)/(3650 \ Hours) = 2136988.6 \ W`

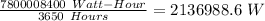
Rate of heat transfer,
`P = (K*A *\delta T)/(L)`

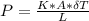
where;

P is the rate of heat transfer (W)

k si the thermal conductivity (W/mk)

ΔT is change in temperature (K)

A is area of the heater (m²)

L is thickness of the heater (m)

`P = (KA(T_2-T_1))/(L) \\\\L = (KA(T_2-T_1))/(P)\\\\L = (385(4.5*3.84)(50-30))/(2136988.6)\\\\L = 0.0623 \ m`

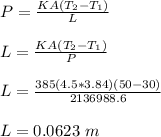
L = 6.23 cm

Therefore, the thickness of the material is 6.23 cm