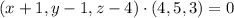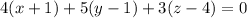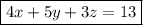Extract the normal vectors from the given planes:
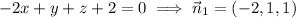

(which are unique up to their signs, meaning either
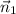 or
or
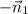 are valid choices for the normal vector)
are valid choices for the normal vector)
The third plane must be perpendicular to both these given planes, which means it would be parallel to both
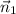 and
and
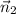 , which in turn means its own normal vector
, which in turn means its own normal vector
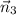 should be perpendicular to both
should be perpendicular to both
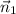 and
and
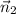 .
.
Enter the cross product:
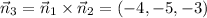
or (4, 5, 3), which also works.
The given plane passes through (-1, 1, 4), so its equation is
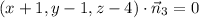
Simplify: