Answer:
Explanation:
Eq.
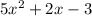
Part A:
1. Set the output value
 (also known as "y" on a coordinate plane) = 0
(also known as "y" on a coordinate plane) = 0
2.
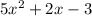 = 0
= 0
3. Factor using "ac" method. (5 x 3 = 15, what factors of 15 when added/subtracted = 2?)
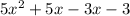 = 0
= 0- 5x(x + 1) - 3(x + 1) = 0
- (5x - 3)(x + 1) = 0
4. Use zero property.
OR
5. These are the x-intercepts: (3/5, 0) and (- 1, 0)
Part B:
Vertex Formula: x = -b/2a
In a quadratic equation the base equation (standard form) is ax^2 + bx + c, where a is a non-zero constant, and b and c are real numbers.
(eq. 5x^2 + 2x - 3)
-2/2(5) = -2/10 = - 1/5 --> x-coordinate
plug (- 1/5) in for x to get - 16/5 as the y-coordinate.
VERTEX: (-1/5, - 16/5) ; minimum because "a" value is positive